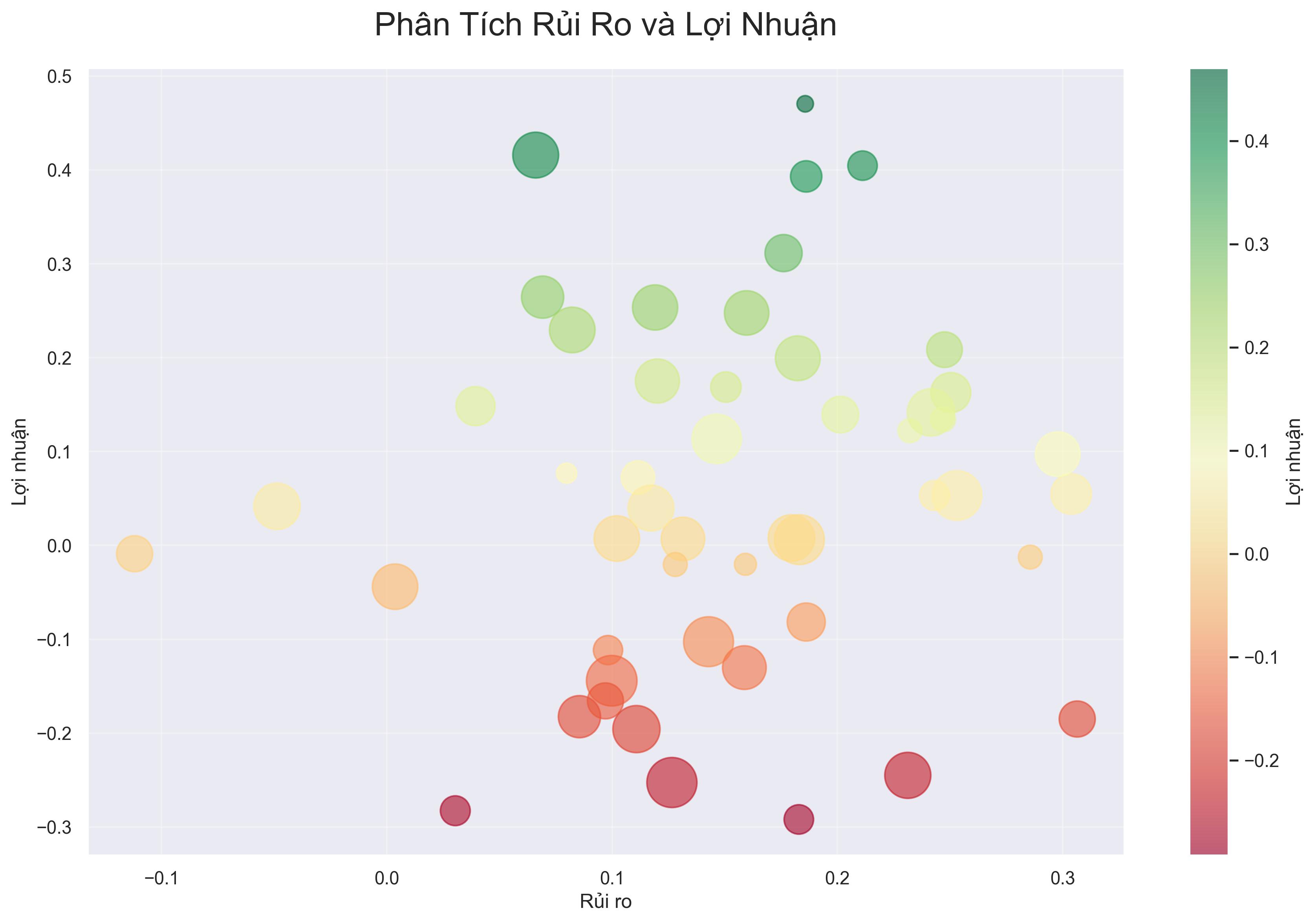
Hệ thống quản lý rủi ro
Trong bài viết này, chúng ta sẽ tìm hiểu cách xây dựng hệ thống quản lý rủi ro hiệu quả cho bot giao dịch tự động.
Đánh giá rủi ro
1. Rủi ro thị trường
class MarketRiskAnalyzer:
def __init__(self):
self.risk_metrics = {}
def calculate_var(self, returns, confidence_level=0.95):
"""Tính toán Value at Risk"""
return np.percentile(returns, (1 - confidence_level) * 100)
def calculate_expected_shortfall(self, returns, var):
"""Tính toán Expected Shortfall (CVaR)"""
return returns[returns <= var].mean()
def analyze_market_risk(self, portfolio):
# Phân tích rủi ro thị trường
returns = self.calculate_returns(portfolio)
var = self.calculate_var(returns)
es = self.calculate_expected_shortfall(returns, var)
return {
'var': var,
'expected_shortfall': es,
'volatility': returns.std()
}
2. Rủi ro tín dụng
class CreditRiskAnalyzer:
def __init__(self):
self.credit_limits = {}
def check_credit_risk(self, counterparty, amount):
"""Kiểm tra rủi ro tín dụng"""
if counterparty not in self.credit_limits:
return False
current_exposure = self.get_current_exposure(counterparty)
return current_exposure + amount <= self.credit_limits[counterparty]
def update_credit_limits(self, counterparty, new_limit):
"""Cập nhật hạn mức tín dụng"""
self.credit_limits[counterparty] = new_limit
Kiểm soát rủi ro
1. Giới hạn vị thế
class PositionLimiter:
def __init__(self, max_position_size, max_leverage):
self.max_position_size = max_position_size
self.max_leverage = max_leverage
def check_position_limit(self, symbol, size, price):
"""Kiểm tra giới hạn vị thế"""
position_value = size * price
# Kiểm tra kích thước vị thế
if position_value > self.max_position_size:
return False
# Kiểm tra đòn bẩy
leverage = position_value / self.get_account_equity()
if leverage > self.max_leverage:
return False
return True
2. Quản lý Stop Loss
class StopLossManager:
def __init__(self, max_loss_percent):
self.max_loss_percent = max_loss_percent
def calculate_stop_loss(self, entry_price, position_type):
"""Tính toán mức stop loss"""
if position_type == 'long':
return entry_price * (1 - self.max_loss_percent)
else:
return entry_price * (1 + self.max_loss_percent)
def check_stop_loss(self, current_price, stop_loss, position_type):
"""Kiểm tra điều kiện stop loss"""
if position_type == 'long':
return current_price <= stop_loss
else:
return current_price >= stop_loss
Giám sát rủi ro
1. Cảnh báo thời gian thực
class RiskMonitor:
def __init__(self):
self.risk_thresholds = {}
self.alert_channels = {}
def monitor_risk_metrics(self, metrics):
"""Giám sát các chỉ số rủi ro"""
alerts = []
for metric, value in metrics.items():
if metric in self.risk_thresholds:
threshold = self.risk_thresholds[metric]
if value > threshold:
alerts.append({
'metric': metric,
'value': value,
'threshold': threshold
})
return alerts
def send_alerts(self, alerts):
"""Gửi cảnh báo"""
for alert in alerts:
for channel, send_func in self.alert_channels.items():
send_func(alert)
2. Báo cáo rủi ro
class RiskReporter:
def __init__(self):
self.report_templates = {}
def generate_risk_report(self, risk_metrics, time_period):
"""Tạo báo cáo rủi ro"""
report = {
'timestamp': datetime.now(),
'period': time_period,
'metrics': risk_metrics,
'summary': self.summarize_risk_metrics(risk_metrics)
}
return report
def summarize_risk_metrics(self, metrics):
"""Tóm tắt các chỉ số rủi ro"""
return {
'highest_risk': max(metrics.items(), key=lambda x: x[1]),
'risk_trend': self.calculate_risk_trend(metrics)
}
Giảm thiểu rủi ro
1. Hedging
class HedgingManager:
def __init__(self):
self.hedging_instruments = {}
def calculate_hedge_ratio(self, position, hedge_instrument):
"""Tính toán tỷ lệ hedge"""
correlation = self.calculate_correlation(position, hedge_instrument)
return correlation * (position.volatility / hedge_instrument.volatility)
def execute_hedge(self, position, hedge_instrument, ratio):
"""Thực hiện hedge"""
hedge_size = position.size * ratio
return self.place_hedge_order(hedge_instrument, hedge_size)
2. Đa dạng hóa
class PortfolioDiversifier:
def __init__(self):
self.correlation_matrix = {}
def calculate_diversification_benefit(self, portfolio):
"""Tính toán lợi ích đa dạng hóa"""
portfolio_risk = self.calculate_portfolio_risk(portfolio)
individual_risks = sum(asset.risk for asset in portfolio.assets)
return 1 - (portfolio_risk / individual_risks)
def optimize_diversification(self, portfolio):
"""Tối ưu hóa đa dạng hóa"""
weights = self.calculate_optimal_weights(portfolio)
return self.rebalance_portfolio(portfolio, weights)
Best Practices
- Thiết lập các giới hạn rủi ro rõ ràng
- Thực hiện kiểm tra rủi ro thường xuyên
- Duy trì hệ thống cảnh báo hiệu quả
- Cập nhật chiến lược giảm thiểu rủi ro
- Lưu trữ và phân tích dữ liệu rủi ro
Kết luận
Hệ thống quản lý rủi ro là thành phần không thể thiếu trong việc vận hành bot giao dịch. Trong bài viết tiếp theo, chúng ta sẽ tìm hiểu về cách xây dựng hệ thống backtesting cho chiến lược giao dịch.